Hyperbolic Language Connection of Words. 2012-2020
07/04/2020 22:56
Hyperbolic Language Connection of Words. 2012-2020
Connection of Words
1.
C is complex plane.
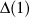 is unit disk which center is the origin of C.
is unit disk which center is the origin of C.
z, w are the two points of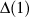 .Hyperbolic distance
.Hyperbolic distance 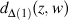 between z and w are defined by the next.
between z and w are defined by the next.
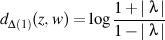 ,
, 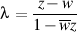 .
.
C is complex plane.
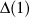 is unit disk which center is the origin of C.
is unit disk which center is the origin of C.z, w are the two points of
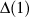 .Hyperbolic distance
.Hyperbolic distance 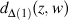 between z and w are defined by the next.
between z and w are defined by the next.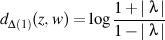 ,
, 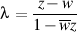 .
.2.
M is complex manifold.
x, y are arbitrary points of M.
fv is finite sequence of regular curve.
Point zv is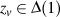 .
.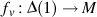 ,
, 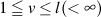 .
.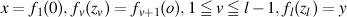 .{
.{ 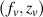 } is called regular chain.Kobayashi pseudodistance dM is defined by the next.
} is called regular chain.Kobayashi pseudodistance dM is defined by the next.
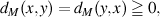
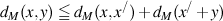 .
.
M is complex manifold.
x, y are arbitrary points of M.
fv is finite sequence of regular curve.
Point zv is
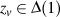 .
.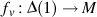 ,
, 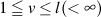 .
.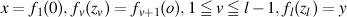 .{
.{ 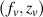 } is called regular chain.Kobayashi pseudodistance dM is defined by the next.
} is called regular chain.Kobayashi pseudodistance dM is defined by the next.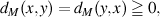
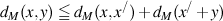 .
.3.
[Interpretation on 2.]
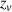 := Meaning minimum of word.dM := Distance of word.
:= Meaning minimum of word.dM := Distance of word.
M:= Word.
[Interpretation on 2.]
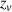 := Meaning minimum of word.dM := Distance of word.
:= Meaning minimum of word.dM := Distance of word.M:= Word.
4.
[Definition]
When dM becomes distance function, M is called Kobayashi hyperbolic.
When dM becomes complete distance, M is called complete Kobayashi hyperbolic.
[Definition]
When dM becomes distance function, M is called Kobayashi hyperbolic.
When dM becomes complete distance, M is called complete Kobayashi hyperbolic.
5.
When M =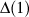 is satisfied at dM , dM is equal to Poincaré distance.
is satisfied at dM , dM is equal to Poincaré distance.
When M =
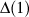 is satisfied at dM , dM is equal to Poincaré distance.
is satisfied at dM , dM is equal to Poincaré distance.6.
X is complex manifold.
M is contained in X as relative compact.
7.
[Definition]
What embedding is hyperbolic embedding is defined by the next.M is KObayashi hyperbolic.
is hyperbolic embedding is defined by the next.M is KObayashi hyperbolic.
Arbitrary boundary points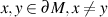 .
.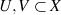 .
.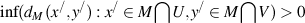 .
.
X is complex manifold.
M is contained in X as relative compact.
7.
[Definition]
What embedding
 is hyperbolic embedding is defined by the next.M is KObayashi hyperbolic.
is hyperbolic embedding is defined by the next.M is KObayashi hyperbolic.Arbitrary boundary points
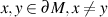 .
.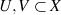 .
.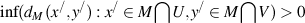 .
.8.
[Theorem,Kwack 1969]
When M is hyperbolicly embedding in X,
What arbitrary regular map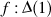 \{0}
\{0} 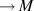 is regularly connected to
is regularly connected to 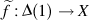 .
.
[Theorem,Kwack 1969]
When M is hyperbolicly embedding in X,
What arbitrary regular map
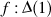 \{0}
\{0} 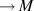 is regularly connected to
is regularly connected to 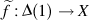 .
.9.
[Interpretation on 6,7,8,9]
X:= Language.
M:= Word.
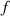 := Distance of word.
:= Distance of word.
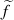 := Connection of words.
:= Connection of words.
[Interpretation on 6,7,8,9]
X:= Language.
M:= Word.
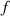 := Distance of word.
:= Distance of word.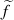 := Connection of words.
:= Connection of words.10.
[Conjecture, Kobayashi]
(i) If d is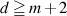 , degree d's general hypersurface X of
, degree d's general hypersurface X of 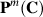 is Kobayashi hyperbolic.(ii)If d is
is Kobayashi hyperbolic.(ii)If d is 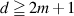 ,
, 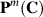 \
\ 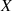 is hyperbolicly embedded in
is hyperbolicly embedded in 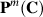 .
.
[Conjecture, Kobayashi]
(i) If d is
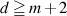 , degree d's general hypersurface X of
, degree d's general hypersurface X of 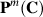 is Kobayashi hyperbolic.(ii)If d is
is Kobayashi hyperbolic.(ii)If d is 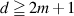 ,
, 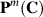 \
\ 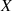 is hyperbolicly embedded in
is hyperbolicly embedded in 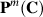 .
.11.
[Interpretation on 10.]
X:= Language.
d:= Hierarchy of language.
[Interpretation on 10.]
X:= Language.
d:= Hierarchy of language.
12.
[References]
<On meaning minimum of word>
From Cell to Manifold / Cell Theory / Tokyo June 2, 2007
Amplitude of Meaning Minimum / Complex Manifold Deformation Theory / Tokyo December 17, 2008
<On distance of word>
Distance Theory /Tokyo May 5, 2004
Distance of Word / Complex Manifold Deformation Theory / Tokyo November 30, 2008
<On connection of words>
Quantum Theory for Language / Tokyo January 15, 2004
<On hyperbolicity>
Reflection of Word / Complex Manifold Deformation Theory / Tokyo December 7, 2008
Boundary of Words / Topological Group language Theory / Tokyo February 12, 2009
[References]
<On meaning minimum of word>
From Cell to Manifold / Cell Theory / Tokyo June 2, 2007
Amplitude of Meaning Minimum / Complex Manifold Deformation Theory / Tokyo December 17, 2008
<On distance of word>
Distance Theory /Tokyo May 5, 2004
Distance of Word / Complex Manifold Deformation Theory / Tokyo November 30, 2008
<On connection of words>
Quantum Theory for Language / Tokyo January 15, 2004
<On hyperbolicity>
Reflection of Word / Complex Manifold Deformation Theory / Tokyo December 7, 2008
Boundary of Words / Topological Group language Theory / Tokyo February 12, 2009
Read more: https://srfl-paper.webnode.com/news/hyperbolic-language-connection-of-words/
Comments
